Many hyperlinks are disabled.
Use anonymous login
to enable hyperlinks.
Overview
| Artifact ID: | b7692adba65535e160e71d67c78be64b97dc01a8 |
|---|---|
| Page Name: | fast sparse integer sets in C |
| Date: | 2017-02-23 19:39:28 |
| Original User: | akupries |
| Mimetype: | text/x-markdown |
| Parent: | 8c32f6e09c90d703e07a280320731d5a8b992ada (diff) |
Content
Up: Notes
References
Excerpts from the first reference:
- Preston Briggs and Linda Torczon's 1993 paper, “An Efficient Representation for Sparse Sets,” describes the trick in detail. Their solution represents the sparse set using an integer array named
denseand an integernthat counts the number of elements indense. Thedensearray is simply a packed list of the elements in the set, stored in order of insertion. If the set contains the elements 5, 1, and 4, thenn = 3anddense[0] = 5,dense[1] = 1,dense[2] = 4:
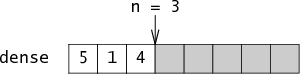
- Together
nanddenseare enough information to reconstruct the set, but this representation is not very fast. To make it fast, Briggs and Torczon add a second array namedsparsewhich maps integers to their indices indense. Continuing the example,sparse[5] = 0,sparse[1] = 1,sparse[4] = 2. Essentially, the set is a pair of arrays that point at each other:
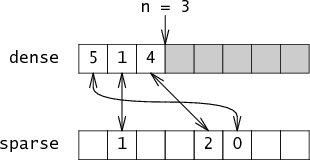
To check whether
iis in the set, you verify that the two arrays point at each other for that element.If
iis not in the set, then it doesn't matter what sparse[i] is set to: eithersparse[i]will be bigger thannor it will point at a value indensethat doesn't point back at it. Either way, we're not fooled.
An important part of this structure is that none of the memory it uses requires initialization before reading from it.
